Table of Contents
cem
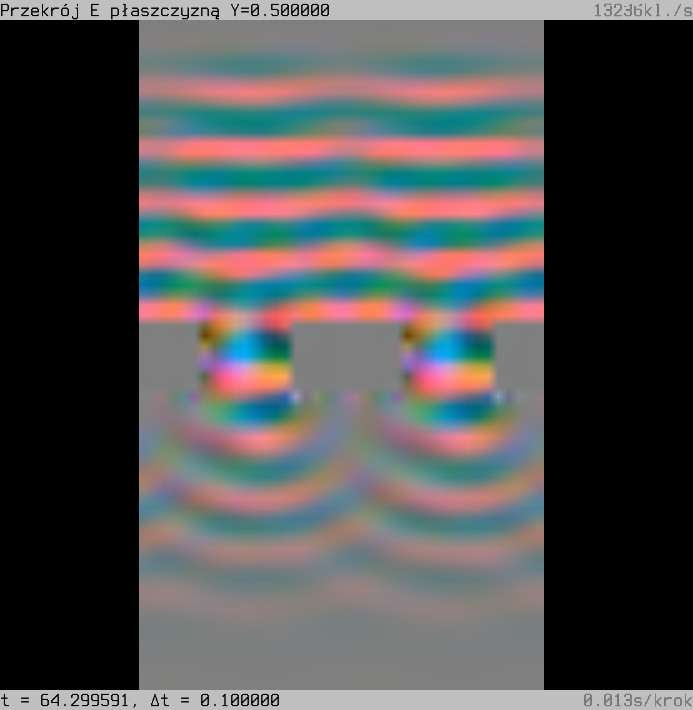
Cem is a simple C implementation of the finite-difference time-domain method for solving Maxwell's equations. It can simulate and visualize a number of wave phenomena like diffraction or refraction.
Background
Written two years after ray, cem got me the first place in the 12th edition of the “Open Interschool Physics Context” in 2015. The thing about this project I'm most proud of is how quickly I completed it. It took me only two weeks to go from having never heard of FDTD to the finished program.
Compiling and running
The source code is available at cem. While considerably more well-written than ray and even has a Makefile, your mileage may vary.
This is a yet another program of mine with an arcane interface. The window displays a cross-section of the (cuboidal) simulation domain. Use the mouse to look around. Keys 1 through 3 switch between orthogonal cross-section planes. Keys 4 through 6 switch between different fields: the electric field, the magnetic field and relative permittivity. F3 opens a new window, so you can look at what's going on from different points of view.
Press return to open the command line. Try “load omkf/1.sim” or the other, bundled files. You can figure out the rest of the commands by looking at the .sim files. Press P and O to start and pause the simulation and press L to take a single step.

![Me presenting at the contest. The text on the slide is a short description of FDTD. [[http://www.lo10.wroc.pl/pl/gala-finalowa-xii-edycji-otwartego-miedzyszkolnego-konkursu-fizycznego-im-bozeny-koronkiewicz.html|Source]] Me presenting at the contest. The text on the slide is a short description of FDTD. [[http://www.lo10.wroc.pl/pl/gala-finalowa-xii-edycji-otwartego-miedzyszkolnego-konkursu-fizycznego-im-bozeny-koronkiewicz.html|Source]]](/lib/exe/fetch.php/cem_presentation.jpg?w=300&tok=b28814)