Table of Contents
Otsu et al. (2018), part 3
In the previous post I explained how PCA can be used to create a convenient basis for representing real-world reflectivities. The procedure uses a set of measured spectra to compute an orthonormal basis, sorted by variance or “statistical significance.” All but the three most significant vectors are then truncated. I called the difference between the actual spectrum and the reconstructed the error term $\pmb\epsilon$.
Naturally the smaller the error, the better. Because $\pmb\epsilon$ is a vector, the authors chose the Euclidean norm (2-norm or L2) to represent the (scalar) error: $$\epsilon = \sqrt{\sum_i \pmb\epsilon_i^2}$$ To get an idea of how well the method works in the general case, the authors would sum up reconstruction errors of all spectra in the dataset. I call this the total error $E$: $$E = \sum_i \epsilon|_{\mathbf s_i}$$ where $\epsilon|_{\mathbf s_i}$ denotes the reconstruction error of $\mathbf s_i$, the $i$-th measured spectrum.
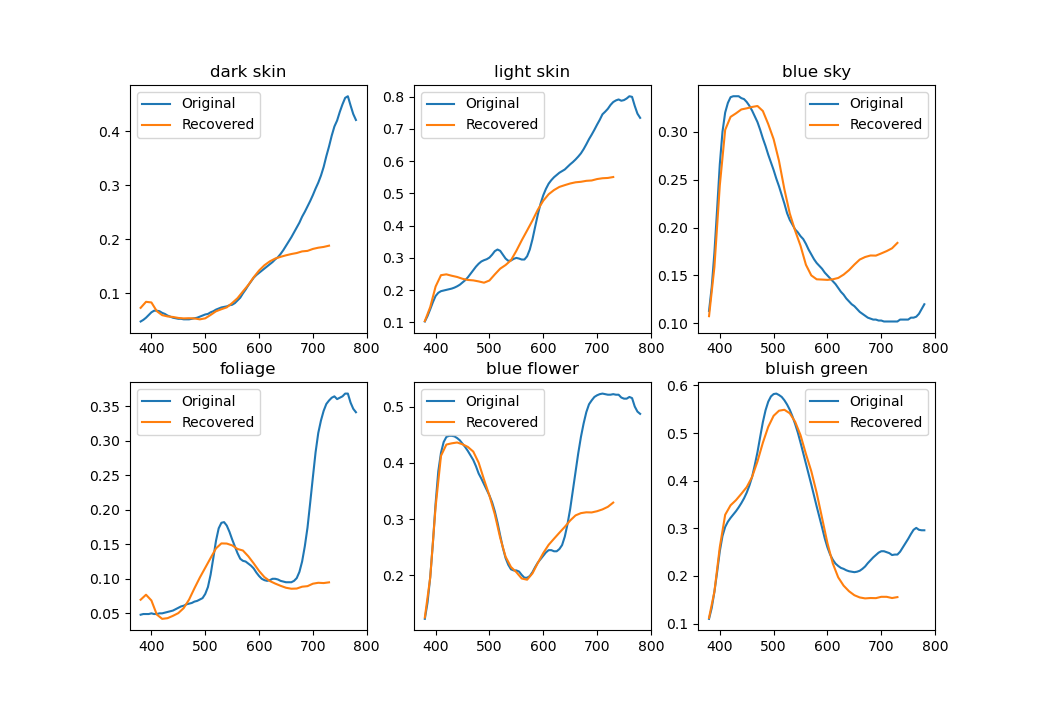
Using just one basis for everything isn't ideal. The picture below shows reconstructions of a few colorchecker spectra. While by definition XYZ tristimulus values (and perceived colors) match perfectly, the spectra aren't that close.
[
]
Clustering
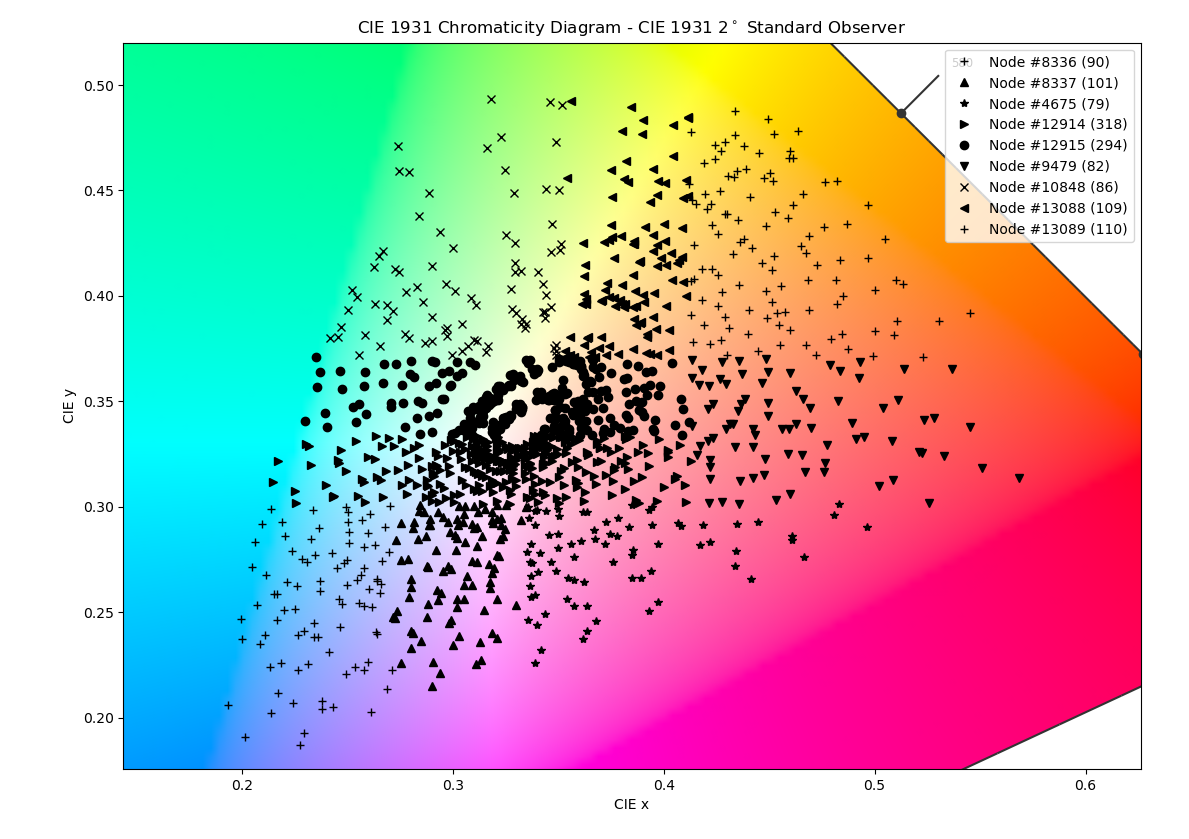
The authors decided to subdivide the CIE 1931 xy space using a binary space partitioning tree. Every node that isn't a leaf divides its subspace in two with a horizontal or vertical line. Leaves, called clusters in the article, contain spectra that lie in their subspace. PCA is done for every cluster separately, creating a set of bases.
[
]
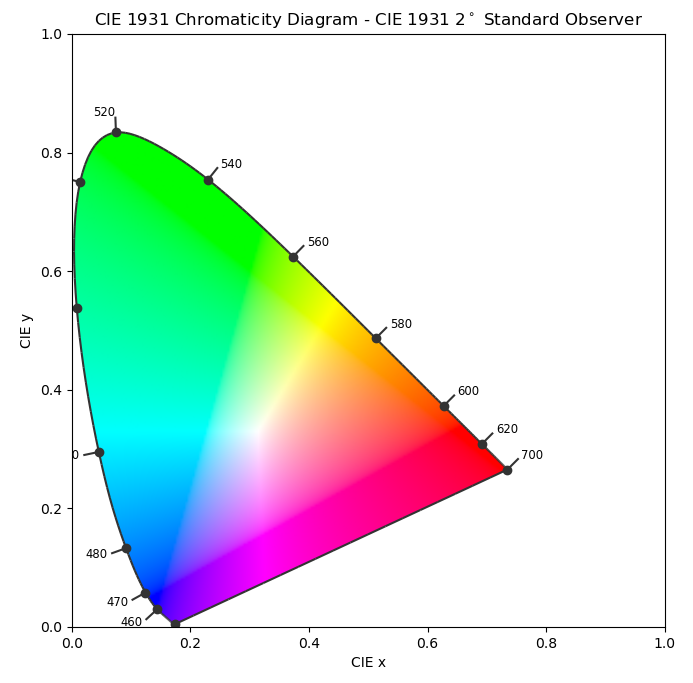
A quick note about CIE 1931 xy chromaticity coordinates. They're derived from CIE 1931 XYZ tristimulus values: $$\begin{cases}
x = \frac{X}{X + Y + Z} \\
y = \frac{Y}{X + Y + Z}
\end{cases}$$ They're often used where only the chromaticity matters and not the lightness $Y$. When plotted, they give rise to the familiar “color triangle” or “horseshoe” diagram, pictured on the right.
The algorithm for creating an optimized clustering is described as follows.
- Search every possible new partitioning in the tree. For every color of every leaf, try partitions with a horizontal and a vertical line going through the color, assigning the color itself to the “lesser” part (to the left or below the line).
- Discard partitions that would create very small nodes. More on this later.
- Compute how each partition would affect the total error of the entire tree (the sum of $E$ of every leaf). Discard those that would increase it.
- Realize the partition that decreases the error the most.
- Repeat the entire process.
The algorithm terminates when no more partitions are possible or there are enough clusters. Authors chose 8 clusters, because of diminishing returns and dataset size concerns. You can look at the original implementation or my code. The article also has a lot more plots and comparison than I post here, so it's definitely worth looking at too.
Below are the results of running my code. I used the entire dataset of 1,279 spectra and optimized for 8 clusters. This takes about 3 hours on my dated i7 3770.
[
]
[
]
Minimum node size
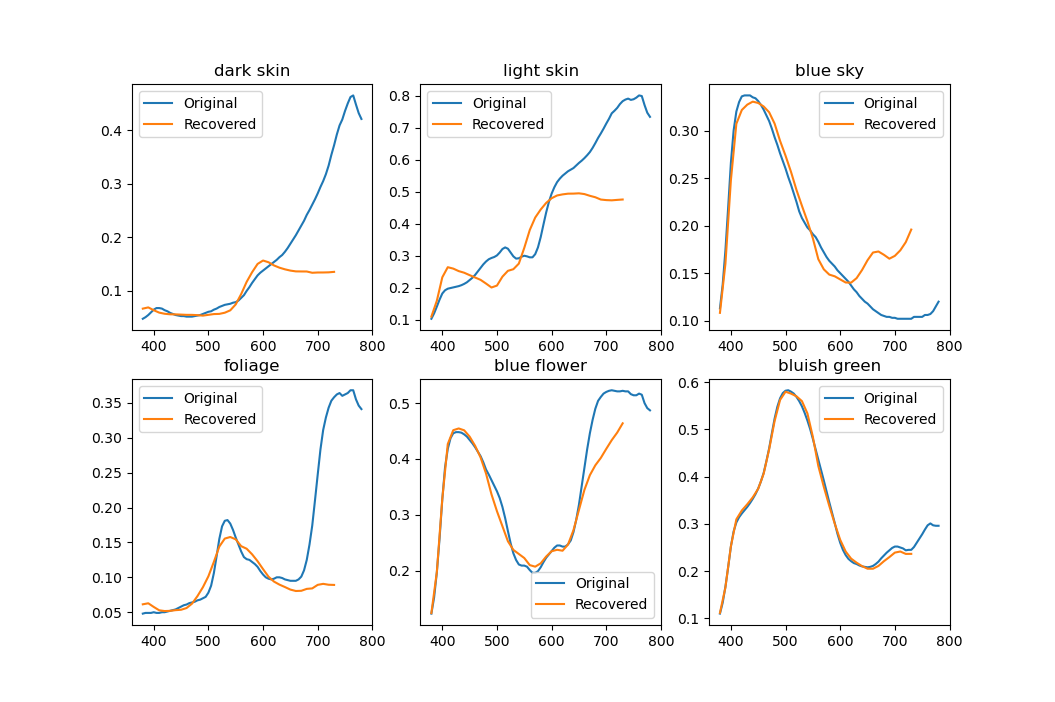
I mentioned that nodes cannot be allowed to be split too finely. First of all, there have to be at least three spectra in a node for PCA to even work. Fewer will result in a singular $M$ and the algorithm simply won't be able to continue. In practice, having few spectra is no good either. Below is a result of PCA decomposition done with just three spectra.
[![PCA decomposition of the first three spectra in Otsu et al.'s dataset. An explanation of what is plotted here is in the [[gsoc:otsu2018_2|previous post]].](/lib/exe/detail.php/gsoc:otsu2018_eigenstates_3_colors.png?id=gsoc%3Aotsu2018_3 "PCA decomposition of the first three spectra in Otsu et al.'s dataset. An explanation of what is plotted here is in the [[gsoc:otsu2018_2|previous post]].")
]
Only two eigenvectors are meaningful and the rest are basically noise. Trying to use this for reconstruction will create completely random-looking spectra, usually going way outside the [0, 1] range. Clearly a lot more data needs to be used to get useful results. In my program I (arbitrarily) set the minimum cluster size to the average cluster size divided by two and it seems to work pretty well. $$\text{min. cluster size} = \left\lfloor\frac{1}{2}\,\frac{\text{num.\,of spectra}}{\text{num.\,of clusters}}\right\rfloor$$
But can reconstructed spectra exceed the allowed [0, 1] range even if the basis is good? Unfortunately yes, and this will be the topic of the next (and the last) post in this series.