Table of Contents
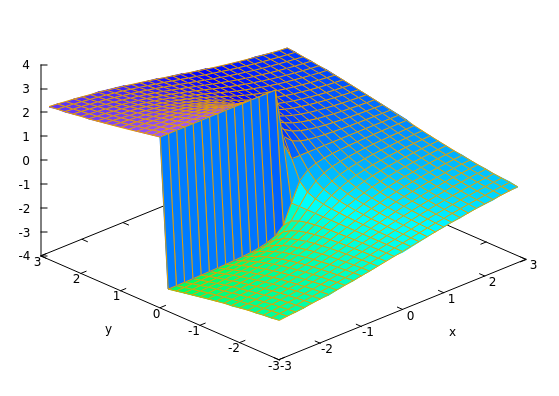
atan2
$$\mathrm{atan2}: \mathbb{R}^2 \setminus (0, 0) \mapsto (-\pi, \pi]$$
$$\mathrm{atan2}(y, x) = \begin{cases}
+\frac{\pi}{2} &: (x = 0) \land (y > 0)
-\frac{\pi}{2} &: (x = 0) \land (y < 0)
\tan^{-1}\frac{y}{x} &: x > 0
\tan^{-1}\frac{y}{x} + \pi &: (x < 0) \land (y \geq 0)
\tan^{-1}\frac{y}{x} - \pi &: (x < 0) \land (y < 0)
\end{cases} $$
where $\tan^{-1} x$ is the principal value of the arctangent, ie. the one in the interval $(-\pi, \pi]$.
Properties
- $\mathrm{atan2}(-y, x) = -\mathrm{atan2}(y, x)$
- $\mathrm{atan2}(cy, cx) = \mathrm{atan2}(y, x)$ for any $c > 0$.
- Discontinuous along $(x < 0) \land (y = 0)$: For any $x < 0$:
- $\lim_{y\to 0^-}\mathrm{atan2}(y, x) = -\pi$
- $\lim_{y\to 0^+}\mathrm{atan2}(y, x) = \pi$
Partial derivatives
The partial derivatives, just like the function itself, are defined everywhere except at the origin. Furthermore, unlike the function, they're not discontinuous along $y = 0$ (except at the origin).
$$ \begin{align}
\frac{\partial}{\partial y} &= \frac{x}{x^2 + y^2}
\frac{\partial}{\partial x} &= \frac{-y}{x^2 + y^2}
\end{align} $$
Interesingly, the function $\tan^{-1}\frac{y}{x}$ has the same partial derivatives.
Systems of equations involving the cosine and the sine of an unknown
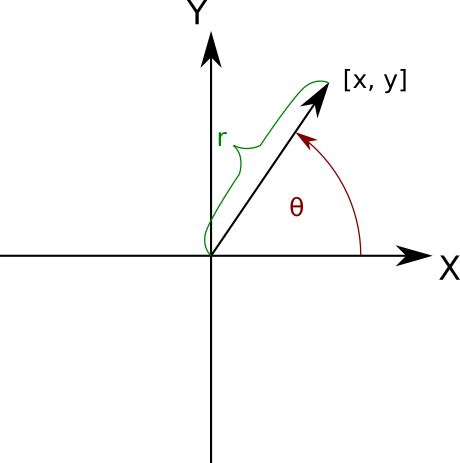
Let $\theta, x, y \in \mathbb{R}$. Consider the following system of equations:
$$ \begin{cases}
\sin{\theta} = y
\cos{\theta} = x
\end{cases} $$
If $x^2 + y^2 = 1$, this system has a unique (up to a multiple of $2\pi$) solution:
$$ \theta = \mathrm{atan2}(y, x) + 2\pi k $$
for any $k \in \mathbb{Z}$. For simplicity k is often set to zero.
Because $\mathrm{atan2}(\sin{\theta}, \cos{\theta}) = \theta$ (up to a multiple of $2\pi$), atan2 can be thought of as the “inverse” of the cosine and sine of the same argument.
C's atan2
The definition at the beginning of this article is suitable for mathematical analysis. However, a more intricate definition is needed for floating-point computation, one that takes signed zeros and infinites into account. The following appears in the C standard:
$$\mathrm{atan2}(y, x) = \begin{cases}
\mathrm{NaN} &: (y = \mathrm{NaN}) \lor (x = \mathrm{NaN})
\pm \pi &: (x < +0) \land (y = \pm 0)
\pm 0 &: (x > +0) \land (y = \pm 0)
-\frac{\pi}{2} &: (x = \pm 0) \land (y < -0)
\frac{\pi}{2} &: (x = \pm 0) \land (y > +0)
\pm \pi &: (x = -0) \land (y = \pm 0)
\pm 0 &: (x = +0) \land (y = \pm 0)
\pi &: (x = -\infty) \land (y > +0) \land (y < +\infty)
-\pi &: (x = -\infty) \land (y < -0) \land (y > -\infty)
+0 &: (x = +\infty) \land (y > +0) \land (y < +\infty)
-0 &: (x = +\infty) \land (y < -0) \land (y > -\infty)
\pm \frac{\pi}{2} &: (x > -\infty) \land (x < +\infty) \land (y = \pm \infty)
\pm \frac{3\pi}{4} &: (x = -\infty) \land (y = \pm \infty)
\pm \frac{\pi}{4} &: (x = +\infty) \land (y = \pm \infty)
\tan^{-1}\frac{y}{x} &: x > +0
\tan^{-1}\frac{y}{x} + \pi &: (x < -0) \land (y \geq 0)
\tan^{-1}\frac{y}{x} - \pi &: (x < -0) \land (y < -0)
\end{cases} $$
In this definition $\mathrm{atan2}(0, 0)$ is not undefined.