Table of Contents
Otsu et al. (2018), part 3
In the previous post I explained how PCA can be used to create a convenient basis for representing real-world reflectivities. The procedure uses a set of measured spectra to compute an orthonormal basis, sorted by variance or “statistical significance.” All but the three most significant vectors are then truncated. I called the difference between the actual spectrum and the reconstructed the error term $\pmb\epsilon$.
Naturally the smaller the error, the better. Because $\pmb\epsilon$ is a vector, the authors chose the Euclidean norm (2-norm or L2) to represent the (scalar) error: $$\epsilon = \sqrt{\sum_i \pmb\epsilon_i^2}$$ To get an idea of how well the method works in the general case, the authors would sum up reconstruction errors of all spectra in the dataset. I call this the total error $E$: $$E = \sum_i \epsilon|_{\mathbf s_i}$$ where $\epsilon|_{\mathbf s_i}$ denotes the reconstruction error of $\mathbf s_i$, the $i$-th measured spectrum.
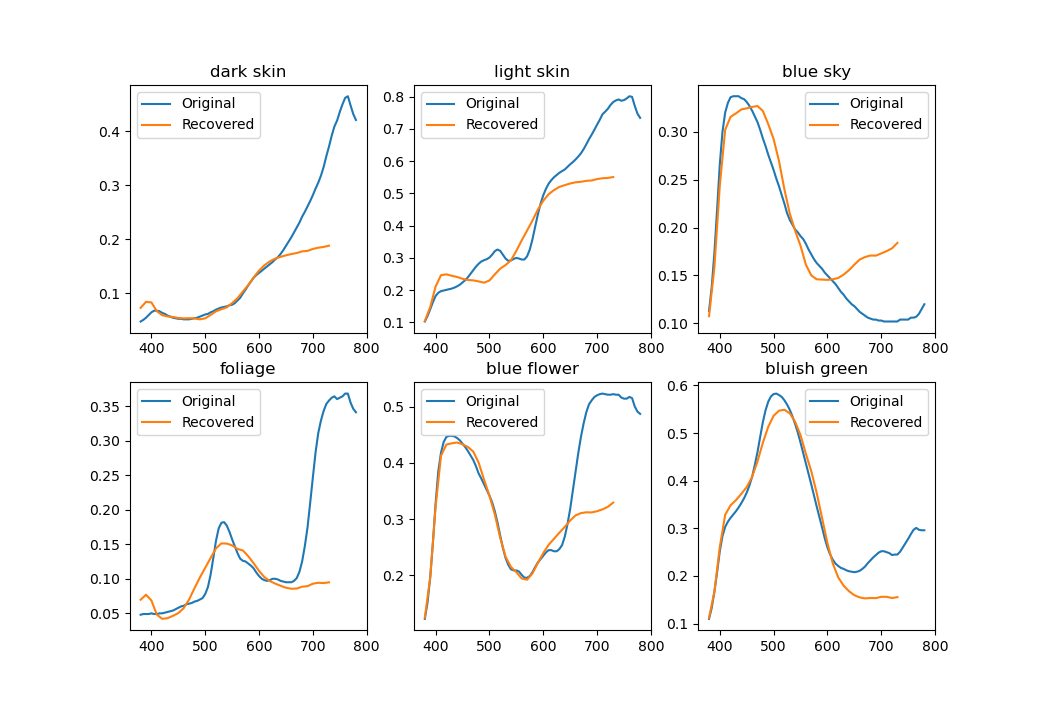
Using just one basis for everything isn't ideal. The picture below shows reconstructions of a few colorchecker spectra. While by definition XYZ tristimulus values (and perceived colors) match perfectly, the spectra aren't that close.
Clustering
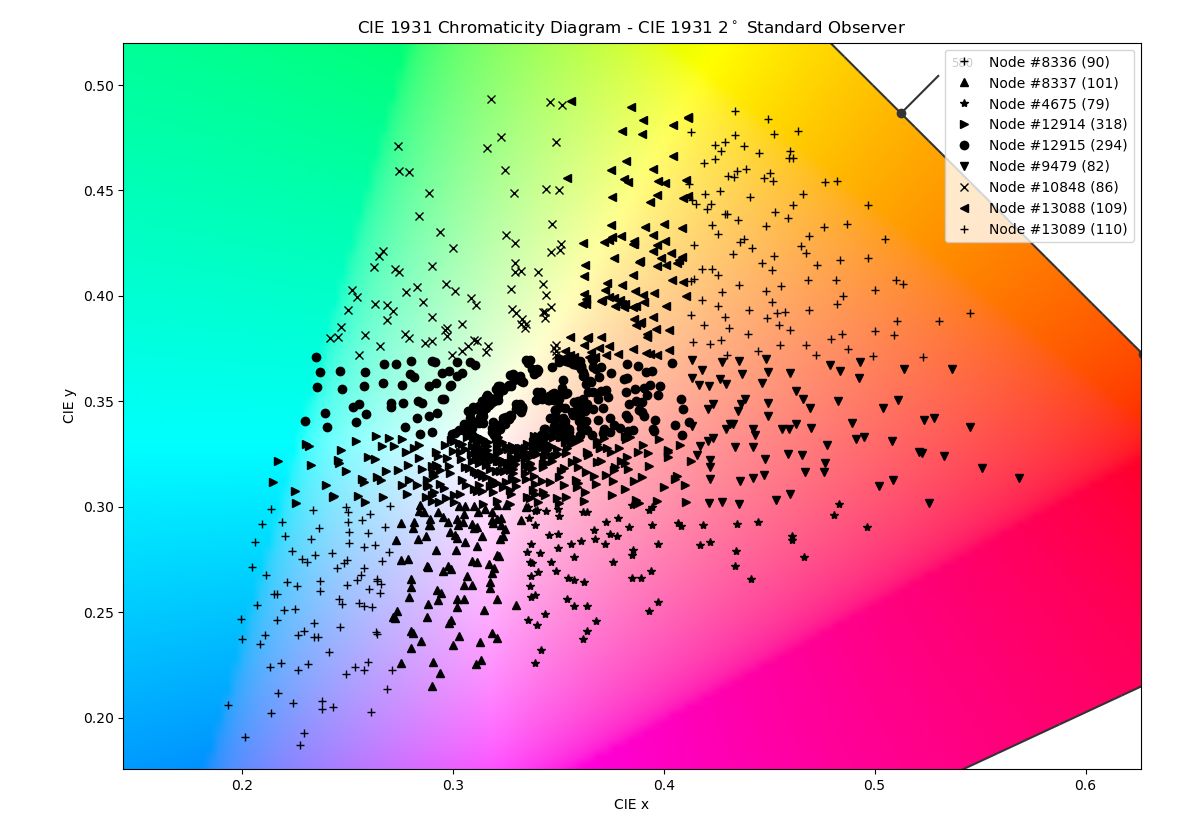
The authors decided to subdivide the CIE 1931 xy space using a binary space partitioning tree. Every node that isn't a leaf divides its subspace in two with a horizontal or vertical line. Leaves, called clusters in the article, contain spectra that lie in their subspace. PCA is done for every cluster separately, creating a set of bases.
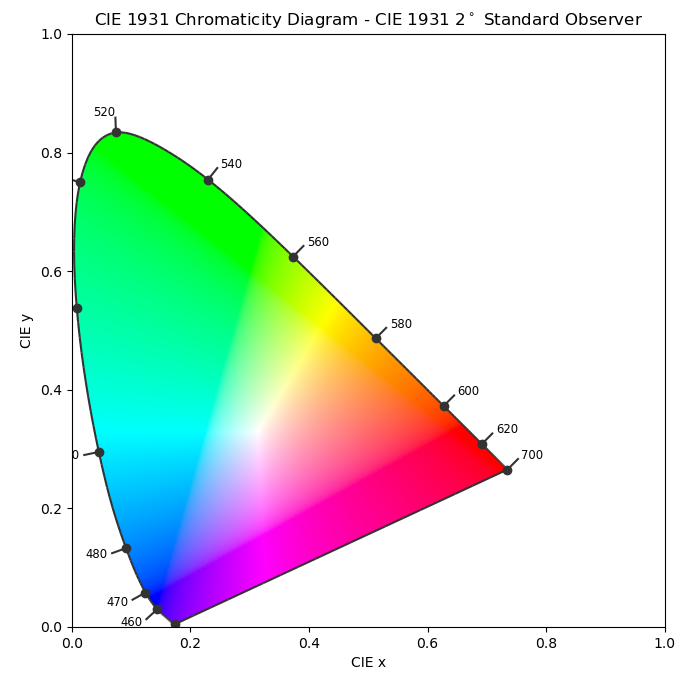
A quick note about CIE 1931 xy chromaticity coordinates. They're derived from CIE 1931 XYZ tristimulus values: $$\begin{cases}
x = \frac{X}{X + Y + Z} \\
y = \frac{Y}{X + Y + Z}
\end{cases}$$ They're often used where only the chromaticity matters and not the lightness $Y$. When plotted, they give rise to the familiar “color triangle” or “horseshoe” diagram, pictured on the right.
The algorithm for creating an optimized clustering is described as follows.
- Search every possible new partitioning in the tree. For every color of every leaf, try partitions with a horizontal and a vertical line going through the color, assigning the color itself to the “lesser” part (to the left or below the line).
- Discard partitions that would create very small nodes. More on this later.
- Compute how each partition would affect the total error of the entire tree (the sum of $E$ of every leaf). Discard those that would increase it.
- Realize the partition that decreases the error the most.
- Repeat the entire process.
The algorithm terminates when no more partitions are possible or there are enough clusters. Authors chose 8 clusters, because of diminishing returns and dataset size concerns. You can look at the original implementation or my code. The article also has a lot more plots and comparison than I post here, so it's definitely worth looking at too.
Below are the results of running my code. I used the entire dataset of 1,279 spectra and optimized for 8 clusters. This takes about 3 hours on my dated i7 3770.
Minimum node size
I mentioned that nodes cannot be allowed to be split too finely. First of all, there have to be at least three spectra in a node for PCA to even work. Fewer will result in a singular $M$ and the algorithm simply won't be able to continue. In practice, having few spectra is no good either. Below is a result of PCA decomposition done with just three spectra.
Only two eigenvectors are meaningful and the rest are basically noise. Trying to use this for reconstruction will create completely random-looking spectra, usually going way outside the [0, 1] range. Clearly a lot more data needs to be used to get useful results. In my program I (arbitrarily) set the minimum cluster size to the average cluster size divided by two and it seems to work pretty well. $$\text{min. cluster size} = \left\lfloor\frac{1}{2}\,\frac{\text{num.\,of spectra}}{\text{num.\,of clusters}}\right\rfloor$$
But can reconstructed spectra exceed the allowed [0, 1] range even if the basis is good? Unfortunately yes, and this will be the topic of the next (and the last) post in this series.

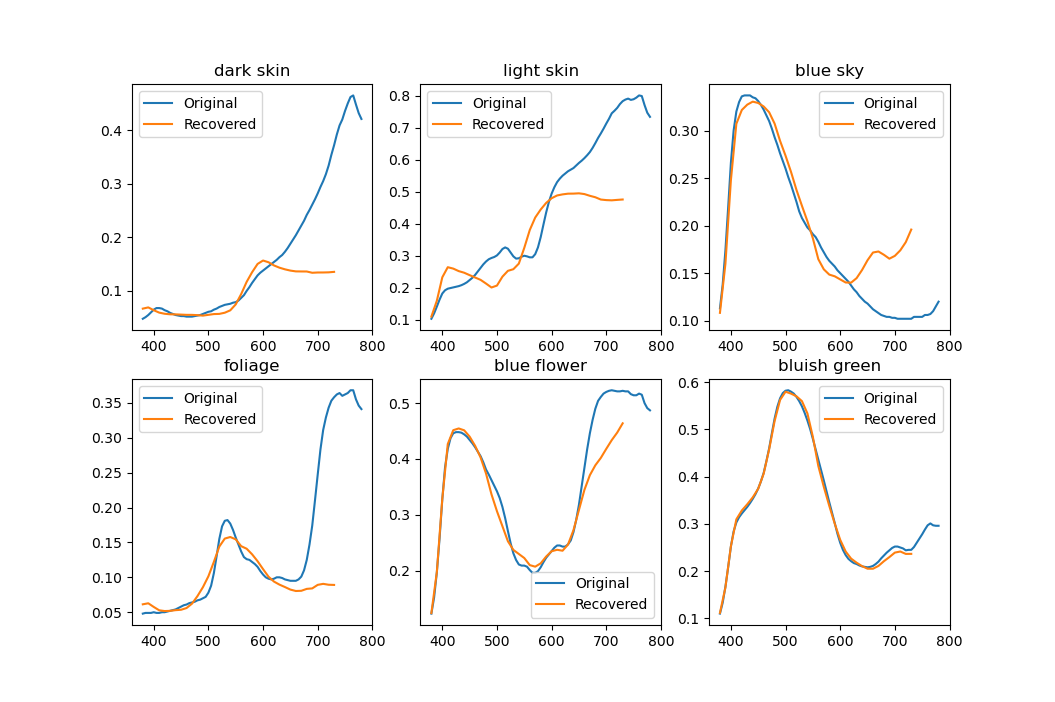
![PCA decomposition of the first three spectra in Otsu et al.'s dataset. An explanation of what is plotted here is in the [[gsoc:otsu2018_2|previous post]]. PCA decomposition of the first three spectra in Otsu et al.'s dataset. An explanation of what is plotted here is in the [[gsoc:otsu2018_2|previous post]].](/lib/exe/fetch.php/gsoc:otsu2018_eigenstates_3_colors.png?w=600&tok=6ec7b9)