Show pagesource

Table of Contents

Ray vs. sphere

A drawing of a ray intersecting a sphere in two dimensions.

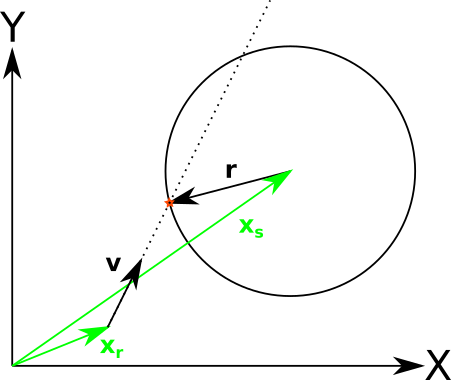
In $\mathbb{R}^N$, a ray of origin $\mathbf{x_r}$ and direction $\mathbf{v}$ and an N-sphere of origin $\mathbf{x_s}$ and radius $r$ intersect at $\mathbf{x}_I$ given by:

$ \mathbf{x}_I = \mathbf{x_r} + t_\pm\mathbf{v} $

where:

$$ \begin{align} t_\pm &= \frac{\mathbf{v} \cdot \mathbf{u} \pm \sqrt{(\mathbf{v} \cdot \mathbf{u})^2 - v^2(u^2 - r^2)}}{v^2} \\ \mathbf{u} &= \mathbf{x_s} - \mathbf{x_r} \end{align} $$

If the expression under the square root is negative, there is no intersection. If it's zero, $t_+ = t_-$ and there is only one intersection.

Notice that since $tv$ is the distance to intersection, $t_-$ corresponds to the closer one and $t_+$ to the further. Depending on the application, you might want to discard negative $t$'s (intersections “behind” the ray).

Surface normal

The surface normal $\mathbf{\hat{n}}$ at an intersection is given by:

$$ \begin{align} \mathbf{r} &= t_\pm\mathbf{v} - \mathbf{u} \\ \mathbf{\hat{n}} &= \mathbf{\hat{r}} \end{align} $$

Normalized v

Notice that the expression for $t_\pm$ becomes appreciably simpler if $v = 1$:

$ t_\pm &= \mathbf{v} \cdot \mathbf{u} \pm \sqrt{(\mathbf{v} \cdot \mathbf{u})^2 - (u^2 - r^2)} $

Derivation

Notice that the point of intersection lies somewhere on the line defined by the ray:

$ \mathbf{x_I} = \mathbf{x_r} + t\mathbf{v}$

for some real $t$. It also lies somewhere on the sphere:

$ \mathbf{x_I} = \mathbf{x_s} + \mathbf{r} $

for some vector $\mathbf{r}$ of length $r$. Combining the two equations and solving for $\mathbf{r}$ yields:

$ \mathbf{x_r} + t\mathbf{v} - \mathbf{x_s} = \mathbf{r} $

To simplify the algebra, substitute $\mathbf{x}_s - \mathbf{x_r} = \mathbf{u}$:

$ t\mathbf{v} - \mathbf{u} = \mathbf{r} $

Since only the length of $\mathbf{r}$ is known, the only thing that can be done at this point is equating the norms of both sides. Squared norms are more convenient in this particular case:

$$ \begin{align} (t\mathbf{v} - \mathbf{u})^2 &= r^2 \\ t^2v^2 + u^2 - 2t\mathbf{v} \cdot \mathbf{u} &= r^2 \\ v^2t^2 - 2\mathbf{v} \cdot \mathbf{u}t + u^2 - r^2 &= 0 \end{align} $$

Solving the quadratic equation and simplifying:

$$ \begin{align} t_\pm &= \frac{2\mathbf{v} \cdot \mathbf{u} \pm \sqrt{4(\mathbf{v} \cdot \mathbf{u})^2 - 4 v^2(u^2 - r^2)}}{2v^2} \\ t_\pm &= \frac{\mathbf{v} \cdot \mathbf{u} \pm \sqrt{(\mathbf{v} \cdot \mathbf{u})^2 - v^2(u^2 - r^2)}}{v^2} \end{align} $$

As with any quadratic equation, there is no real solution if the expression under the square root is negative and if it's zero, the solutions coincide.

Notice that $\mathbf{r}$ is perpendicular to the sphere at an intersection. Normalizing this vector yields the surface normal $\mathbf{\hat{n}}$.