Show pagesource

Table of Contents

Angle between two vectors

Which one to choose?

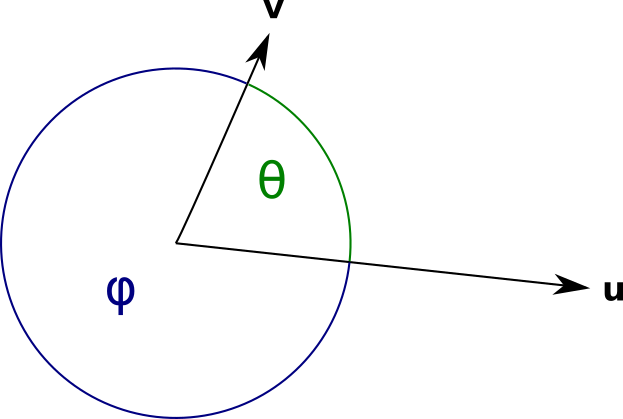
In $\mathbb{R}^n$ there are two angles between any two vectors. The smallest one I'll call $\theta$. The other one, its 360° complement, I'll call $\phi$.

The smallest angle between two vectors $\mathbf{u}$ and $\mathbf{v}$ is given by:

$$ \theta = \cos^{-1}{\frac{\mathbf{u} \cdot \mathbf{v}}{uv}} $$

which follows easily from the geometric definition of the dot product:

$$ \mathbf{u} \cdot \mathbf{v} = uv\cos \theta $$

The other angle is simply the 360° complement:

$$ \phi = 2\pi - \theta $$

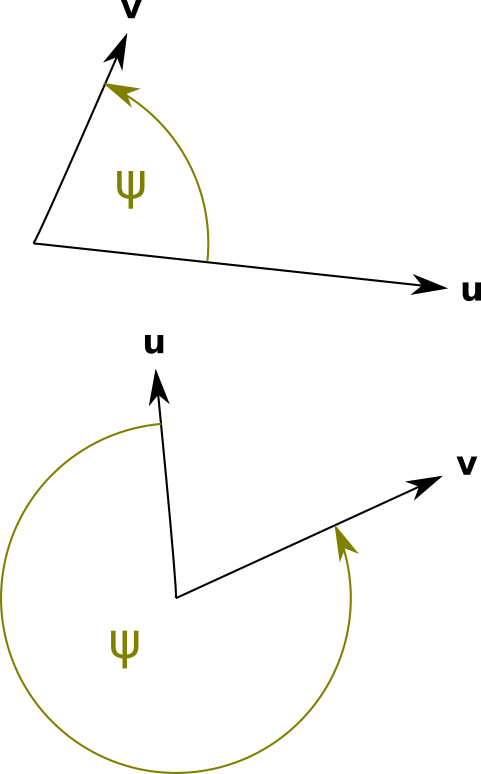
Oriented angle

Oriented angles between example vectors u and v.

Some applications call for the oriented angle $\psi$. It's the angle going from one vector to the other in a specific direction. The convention that I use is that the direction be counter-clockwise.

Because the angle is oriented, changing the order of vectors (or the used convention) changes the angle's sign:

$$\psi(\mathbf{u}, \mathbf{v}) = -\psi(\mathbf{v}, \mathbf{u})$$

or, equivalently:

$$\psi(\mathbf{u}, \mathbf{v}) = 2\pi - \psi(\mathbf{v}, \mathbf{u})$$

Furthermore:

$$\psi({\mathbf{u}, \mathbf{u}) = 0$$

It's also worth noting that:

$$\cos\theta = \cos\phi = \cos\psi$$

which is why the dot product doesn't carry enough information to compute $\psi$.

In two dimensions

In any coordinate system:

$$ \begin{align} \psi(\mathbf{u}, \mathbf{v}) &= \mathrm{atan2}(\mathbf{u} \cross_2 \mathbf{v}, \mathbf{u} \cdot \mathbf{v}) \\ &= \mathrm{atan2}(\mathbf{u}_1\mathbf{v}^2 - \mathbf{u}_2\mathbf{v}^1, \mathbf{u}_1\mathbf{v}^1 + \mathbf{u}_2\mathbf{v}^2) \end{align} $$

Derivation: in two dimensions

Using the geometric definitions of the two-dimensional cross product and the dot product:

$$ \begin{cases} \mathbf{u} \cdot \mathbf{v} = uv\cos \theta \\ \mathbf{u} \cross_2 \mathbf{v} = uv\sin \theta \\ \end{cases} $$

Solving for the sine and cosine:

$$ \begin{cases} \cos \theta = \frac{1}{uv} \mathbf{u} \cdot \mathbf{v} \\ \sin \theta = \frac{1}{uv} \mathbf{u} \cross_2 \mathbf{v} \\ \end{cases} $$

Solving for $\theta$ (see Systems of equations involving the cosine and the sine of an unknown):

$$ \begin{align} \theta &= \mathrm{atan2}\left(\frac{1}{uv}\mathbf{u} \cross_2 \mathbf{v}, \frac{1}{uv}\mathbf{u} \cdot \mathbf{v}\right) \\ &= \mathrm{atan2}(\mathbf{u} \cross_2 \mathbf{v}, \mathbf{u} \cdot \mathbf{v}) \end{align} $$

The simplification can be done because $\frac{1}{uv} > 0$ and eliminating it will not change the result (see properties of atan2).