Table of Contents
Convergence problems
I've been trying to write code that find parameters to the reflectivity model I mentioned in an earlier post. The objective is to minimize the difference between the color given the model and the target. It turns out the optimization is rather difficult and all SciPy solvers (including global optimization algorithms) frequently fail. At the moment I only have a loose idea of what's going on.
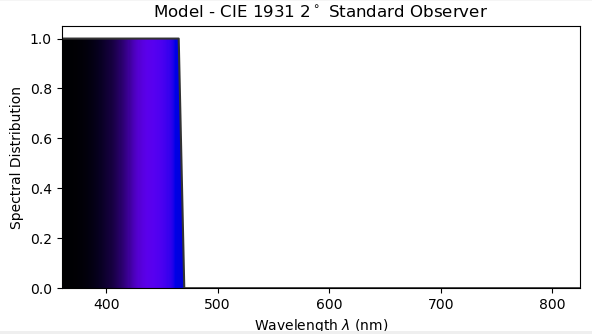
Because of the sigmoid function used in the model, very large coefficients create spectra resembling a rectangular or a step function (like on the picture). Then, it's always possible to adjust the coefficients to make the spectrum even steeper without changing its overall shape. After doing this enough times, coefficients are so large that varying them barely changes the spectrum, a situation solvers treat as having found a good minimum. I suppose it's because the gradient becomes very small, but a better-suited algorithm would look at the near-zero Hessian and notice it's moving along an asymptote (a bad minimum here). I'm also not sure why solvers are (sometimes) attracted to big numbers in the first place.
I did manage to overcome this issue, but in a rather hacky and inelegant way described below.
Feedback
Because the end goal is to reproduce Jakob and Hanika's rather dense coefficient maps, consisting of almost 800,000 points per color space, coefficients from nearby, already-solved-for colors can be used as starting points. This greatly improves the chances of finding a good minimum. Coefficients for unsaturated (but not too dark) colors are easy to find, so they provide good starting points for the entire feedback scheme.
Unfortunately there are still some edge cases where the solver will fail even if it's given a good starting point.
A more general solution
To make sure I'll always be able to find the coefficients, I came up with a simple algorithm. Whenever optimization fails, a color with known coefficients is used to solve for a point somewhere between the target and the color. The process is repeated, getting closer and closer to the target until it finally converges. Below is an example using test_bad_convergence.py.
{|
! XYZ ! Starting coeffs. ! Final coeffs. ! ΔE
The algorithm backtracks a lot, but it does eventually converge. It also highlights a significant problem with the implementation. This particular example runs about 3 orders of magnitude slower than the authors' code.
What next?
Thomas and I agreed that despite the horrible performance, the code is usable enough. The next step is writing code that would allow users to sample precomputed tables. I'll come back to the problem of creating the tables themselves later.